Given a protein interaction network G=(V,E) and a protein u∈V, let N be the total number of nodes in the network,
Nu be the set of neighbors of node u, and A=a(u,v) be the adjacency matrix of the network.
If node u doesn't interact with node v, a(u,v)=0; otherwise, a(u,v)=1. So the formulas of the centrality methods are shown as
the following:
DC (Degree Centrality)
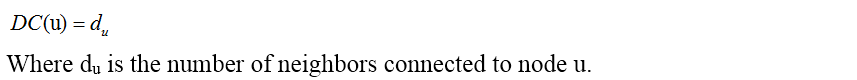 Jeong H, Mason S P, Barabasi A L, et al. Lethality and centrality in protein networks[J]. Nature, 2001, 411(6833): 41-42.
Jeong H, Mason S P, Barabasi A L, et al. Lethality and centrality in protein networks[J]. Nature, 2001, 411(6833): 41-42.
View Article
BC (Betweenness Centrality)
 Joy M P, Brock A, Ingber D E, et al. High-betweenness proteins in the
yeast protein interaction network[J]. BioMed Research International, 2005, 2005(2): 96-103.
Joy M P, Brock A, Ingber D E, et al. High-betweenness proteins in the
yeast protein interaction network[J]. BioMed Research International, 2005, 2005(2): 96-103.
View Article
CC (Closeness Centrality)
 Wuchty S, Stadler P F. Centers of complex networks[J]. Journal of Theoretical Biology, 2003, 223(1): 45-53.
Wuchty S, Stadler P F. Centers of complex networks[J]. Journal of Theoretical Biology, 2003, 223(1): 45-53.
View Article
EC (Eigenvector Centrality)
 Bonacich P. Power and centrality: A family of measures[J]. American journal of sociology, 1987: 1170-1182.
Bonacich P. Power and centrality: A family of measures[J]. American journal of sociology, 1987: 1170-1182.
View Article
IC (Information Centrality)
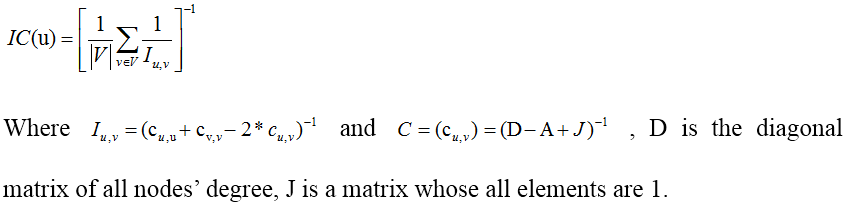 Stephenson K, Zelen M. Rethinking centrality: Methods and examples[J]. Social Networks, 1989, 11(1): 1-37.
Stephenson K, Zelen M. Rethinking centrality: Methods and examples[J]. Social Networks, 1989, 11(1): 1-37.
View Article
LAC (Local Average Connectivity-based method)
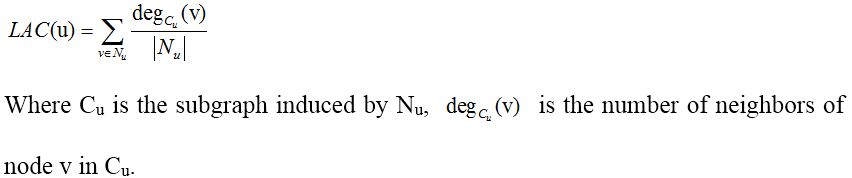 Li M, Wang J, Chen X, et al. A local average connectivity-based method for identifying essential proteins
from the network level[J]. Computational biology and chemistry, 2011, 35(3): 143-150.
Li M, Wang J, Chen X, et al. A local average connectivity-based method for identifying essential proteins
from the network level[J]. Computational biology and chemistry, 2011, 35(3): 143-150.
View Article
NC (Network Centrality)
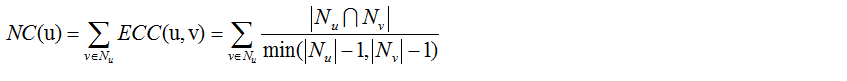 Wang J, Li M, Wang H, et al. Identification of essential proteins based on edge clustering coefficient[J]. IEEE/ACM Transactions on Computational Biology and Bioinformatics, 2012, 9(4): 1070-1080.
Wang J, Li M, Wang H, et al. Identification of essential proteins based on edge clustering coefficient[J]. IEEE/ACM Transactions on Computational Biology and Bioinformatics, 2012, 9(4): 1070-1080.
View Article
SC (Subgraph Centrality)
 Estrada E, Rodriguez-Velazquez J A. Subgraph centrality in complex networks[J]. Physical Review E, 2005, 71(5): 056103.
Estrada E, Rodriguez-Velazquez J A. Subgraph centrality in complex networks[J]. Physical Review E, 2005, 71(5): 056103.
View Article
MNC (Maximum Neighborhood Component)
 Lin C Y, Chin C H, Wu H H, et al. Hubba: hub objects analyzer-a framework of interactome hubs identification for network biology[J]. Nucleic acids research, 2008, 36(suppl 2): W438-W443.
Lin C Y, Chin C H, Wu H H, et al. Hubba: hub objects analyzer-a framework of interactome hubs identification for network biology[J]. Nucleic acids research, 2008, 36(suppl 2): W438-W443.
View Article
DMNC (Density of Maximum Neighborhood Component)
 Lin C Y, Chin C H, Wu H H, et al. Hubba: hub objects analyzer-a framework of interactome hubs identification for network biology[J]. Nucleic acids research, 2008, 36(suppl 2): W438-W443.
Lin C Y, Chin C H, Wu H H, et al. Hubba: hub objects analyzer-a framework of interactome hubs identification for network biology[J]. Nucleic acids research, 2008, 36(suppl 2): W438-W443.
View Article
Lindex (Lobby Index)
 Korn A, Schubert A, Telcs A. Lobby index in networks[J]. Physica A: Statistical Mechanics and its Applications, 2009, 388(11): 2221-2226.
Korn A, Schubert A, Telcs A. Lobby index in networks[J]. Physica A: Statistical Mechanics and its Applications, 2009, 388(11): 2221-2226.
View Article
PageRank
 Kim S J, Lee S H. An improved computation of the pagerank algorithm[C]//European Conference on Information Retrieval. Springer Berlin Heidelberg, 2002: 73-85.
Kim S J, Lee S H. An improved computation of the pagerank algorithm[C]//European Conference on Information Retrieval. Springer Berlin Heidelberg, 2002: 73-85.
View Article
LeaderRank
 Lu L, Zhang Y C, Yeung C H, et al. Leaders in social networks, the delicious case[J]. PloS one, 2011, 6(6): e21202.
Lu L, Zhang Y C, Yeung C H, et al. Leaders in social networks, the delicious case[J]. PloS one, 2011, 6(6): e21202.
View Article
ECC(Eccentricity)
 Hage P, Harary F. Eccentricity and centrality in networks. Social Networks, 1995, 17: 57-63.
Hage P, Harary F. Eccentricity and centrality in networks. Social Networks, 1995, 17: 57-63.
View Article
SLC(Semi-local Centrality)
 Chen D B, Lv L, Shang M S, et al. Identifying influential nodes in complex networks. Physica A, 2012, 391: 1777-1787.
Chen D B, Lv L, Shang M S, et al. Identifying influential nodes in complex networks. Physica A, 2012, 391: 1777-1787.
View Article
LBC(Localized Bridging Centrality)
 Nanda S, Kotz D. Localized Bridging Centrality for Distributed Network Analysis. 2008:62-67.
Nanda S, Kotz D. Localized Bridging Centrality for Distributed Network Analysis. 2008:62-67.
View Article
NeiC(Neighborhood Connectivity)
 Maslov S, Sneppen K. Specificity and stability in topology of protein networks. Science, 2002, 296(5569):910-913.
Maslov S, Sneppen K. Specificity and stability in topology of protein networks. Science, 2002, 296(5569):910-913.
View Article
DSP
 Pengxiang Li, Yuqing Ren, Youmin Xi. A measure of the importance of network nodes (sets). Systems engineering,2004,22(4):13-20.
Pengxiang Li, Yuqing Ren, Youmin Xi. A measure of the importance of network nodes (sets). Systems engineering,2004,22(4):13-20.
View Article
MDD
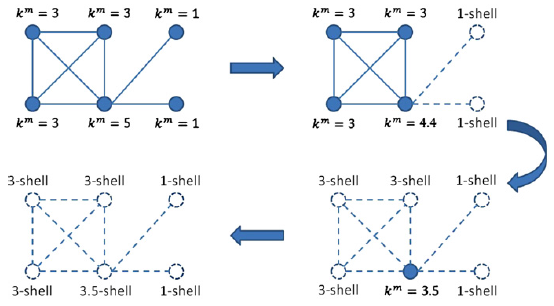 An Zeng, Cheng-Jun Zhang, Ranking spreaders by decomposing complex networks, Physics Letters A, Volume 377, Issue 14,2013,Pages 1031-1035.
An Zeng, Cheng-Jun Zhang, Ranking spreaders by decomposing complex networks, Physics Letters A, Volume 377, Issue 14,2013,Pages 1031-1035.
View Article
LCCDC
 Natarajan Meghanathan. A computationally lightweight and localized centrality metric in lieu of betweenness centrality for complex network analysis.Vietnam Journal of Computer Science, 2017, Volume 4, Number 1, Page 23-38.
Natarajan Meghanathan. A computationally lightweight and localized centrality metric in lieu of betweenness centrality for complex network analysis.Vietnam Journal of Computer Science, 2017, Volume 4, Number 1, Page 23-38.
View Article
WHC
 Yu S, Gao L, Wang Y F, et al. Weighted H-index for identifying influential spreaders. 2017.
Yu S, Gao L, Wang Y F, et al. Weighted H-index for identifying influential spreaders. 2017.
View Article
KShell
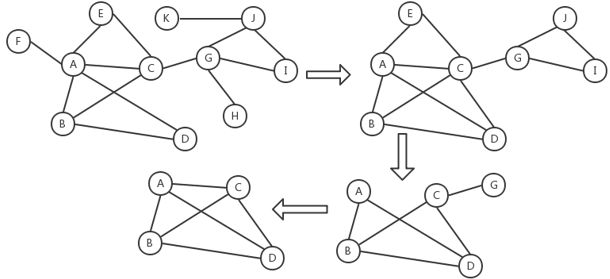 Kitsak M, Gallos L K, Havlin S, et al. Identification of influential spreaders in complex networks. Nat Phys, 2010, 6:888-893
Kitsak M, Gallos L K, Havlin S, et al. Identification of influential spreaders in complex networks. Nat Phys, 2010, 6:888-893
View Article
MEC
 Tingyuan Nie, Zheng GuoUsing, et al. Using mapping entropy to identify node centrality in complex networks. Physica A, 2016, 456:290-297.
Tingyuan Nie, Zheng GuoUsing, et al. Using mapping entropy to identify node centrality in complex networks. Physica A, 2016, 456:290-297.
View Article